Výpočetní možnosti počítačů umožňují matematikům zobrazovat a prozkoumávat mnohé systémy, které by jinak zůstaly lidským očím skryty.
Výsledné obrázky nemusí mít pouze praktický význam, ale často jsou umělecky zajímavé samy o sobě. V tomto textu si ukážeme čtyři příklady výpočtů se zajímavými vizualizacemi, které by bez použití počítače nebylo prakticky možné vytvořit.
Při tvorbě všech zde uvedených obrázků byl použit programovací jazyk Julia. Pro případné zájemce jsou k dispozici zdrojové kódy ve volně dostupném GitHub repozitáři https://github.com/kalvotom/julia-examples. Lze tedy s obrázky dále snadno experimentovat.
1. Mandelbrotova množina
Povídání o umělecky zajímavých výsledcích matematických výpočtů nelze nezačít pravděpodobně nejznámějším příkladem, Mandelbrotovou množinou. Benoit Mandelbrot (1924-2010), matematik polského původu, byl jedním z prvních propagátorů využití počítačové grafiky k zobrazování fraktálních útvarů.
Otázka, kterou se zabýval, je velmi snadno formulovatelná. Pro komplexní číslo c uvažme zobrazení
![]()
Vezměme bod z = 0 ∈ C a opakovaně na něj aplikujme Mc. Ptáme se, zda-li takto vzniknuvší posloupnost komplexních čísel je omezená, nebo neomezená. Pokud je omezená, tak c patří do Mandelbrotovy množiny.
Výše popsaný výpočet samozřejmě nemůžeme doslova provést ani pomocí počítače.Potřebovali bychom totiž vypočíst nekonečný počet členů zmíněné posloupnosti. Není ani možné analyticky rozhodnout, které komplexní c do Mandelbrotovy množiny patří a které ne. Uchýlíme se proto k přibližnému výpočtu.
Programu předepíšeme poloměr a maximální počet iterací zobrazení Mc. Pokud všechny povolené iterace nejsou od počátku dále než předepsaný poloměr prohlásíme c za prvek Mandelbrotovy množiny. Naopak, pokud vzdálenost členu posloupnosti od počátku přeroste uvažovaný poloměr, pak bod c do Mandelbrotovy množiny nepatří.
Tento proces opakujeme pro všechny body jistého obdélníku v komplexní rovině, který jsme rozdělili na pixely dle předepsaného rozlišení. Bodu pak přiřadíme barvu podle toho kolik iterací jsme museli provést, aby iterace opustily předepsaný poloměr. Volba barvy je čistě na naší libovůli a fantazii. Bodům, které patří do Mandelbrotovy množiny pak přiřadíme odlišnou barvu, v našem případě bílou.

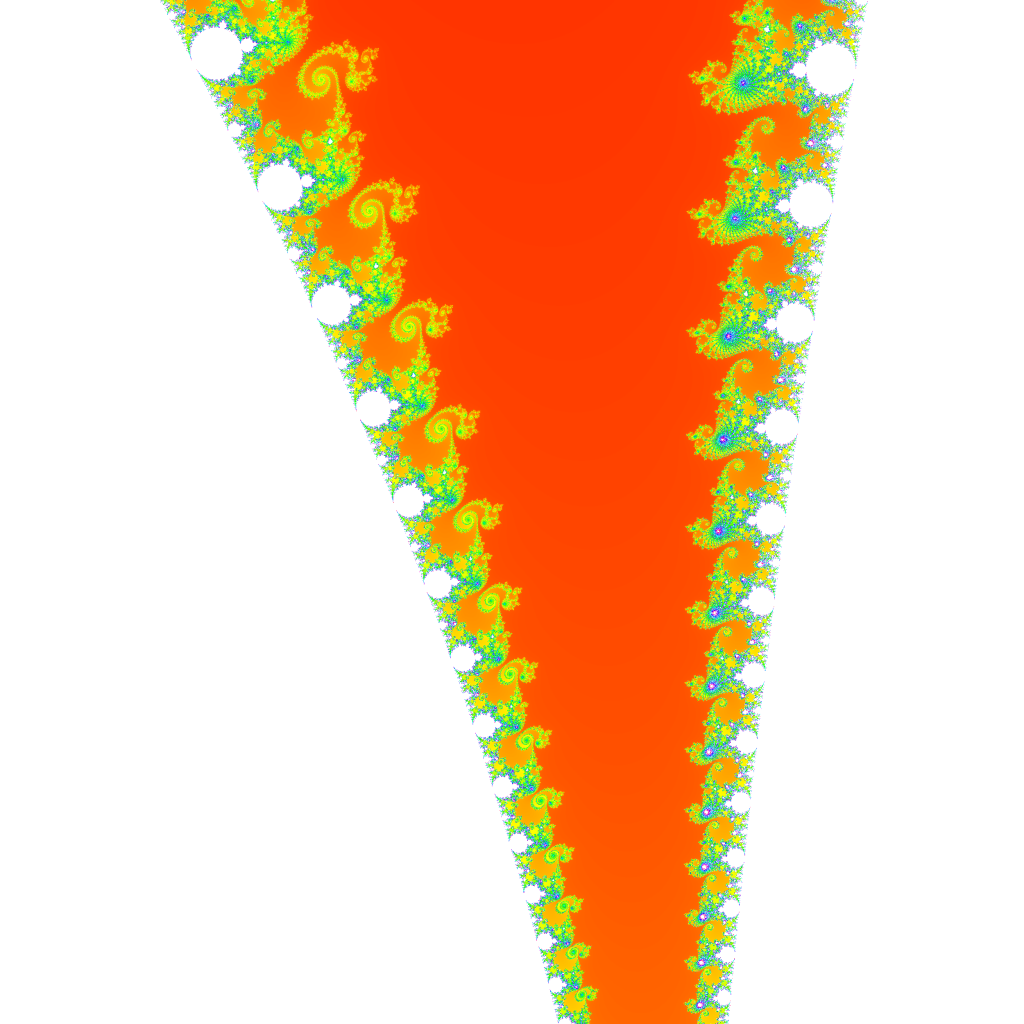
Na obrázku 1 je zobrazen celkový pohled na Mandelbrotovu množinu (bílá oblast). Je velmi překvapivé, že z tak jednoduchého pravidla může vzniknout tak komplikovaná množina. Na obrázcích 2 a 3 jsou pak zobrazeny zajímavé výřezy a přiblížení Mandelbrotovy množiny.

2. Číslo π
Číslo π označuje poměr délky obvodu libovolného kruhu ku jeho průměru, nebo alternativně poměr obsahu kruhu ku kvadrátu jeho poloměru. Lidé ho znají, používají a studují nejen kvůli jeho praktickému významu již od antiky. Jedná se o iracionální a transcendentní číslo s nekonečným neperiodickým desetinným rozvojem. Jeho několik prvních, čtenáři jistě dobře známých, cifer je
π = 3.14159 . . .
V Čechách je toto číslo známo i jako Ludolfovo číslo. K výpočtu cifer čísla π totiž přispěl i německý matematik Ludolf van Ceulen (1540–1610), který vypočetl jeho prvních 35 cifer. V době psaní tohoto článku je hodnota π známa s přesností na 13 300 000 000 000 cifer.
Hodnotu čísla π lze vizualizovat různými způsoby. Na desetinný rozvoj čísla π se lze dívat jako na posloupnost cifer, tedy čísel 0, 1, . . . , 9. Rozdělme obvod kruhu na deset částí a každé části oblouku přiřaďme jednu cifru a barvu. Pokud spolu v desetinném rozvoji dvě čísla sousedí, spojme odpovídající oblouky barvou danou cifrou více vlevo.
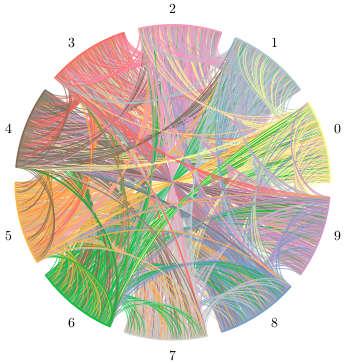
Výsledek tohoto procesu je na obrázku 4, kde jsem vzali do úvahy prvních 2 000 cifer čísla π. Tento obrázek samozřejmě nemá přílišný praktický význam. Zvídavý čtenář si může zkusit představit, jak by vypadal diagram stejného typu pro čísla s periodickým desetinným rozvojem.
3. Fermiho-Ulamův model
Předchozí ukázky vycházely z poměrně abstraktních příkladů (iterace jistého zobrazení v komplexní rovině, velké množství cifer čísla π). Nyní si ukážeme zajímavé obrázky pocházející ze simulací dynamiky relativně jednoduchého fyzikálního systému.
V první polovině minulého století se italský fyzik Ernico Fermi (1901–1954) snažil vysvětli vznik vysoce energetických částic dopadajících na Zemi z vesmíru. Jádro jeho myšlenky spočívalo v představě o náhodném urychlovaní a zpomalovaní elektricky nabitých částic pomocí magnetických polí při jejich cestě vesmírným prostorem. Polský matematik Stanislav Ulam (1909–1984) model značně zjednodušil a umožnil tak jeho zkoumání pomocí v té době dostupných počítačů.
Představte si jednorozměrný hmotný bod, jehož pohyb je omezen mezi dvěma stěnami, z nichž jedna periodicky kmitá. Mezi stěnami se pohybuje rovnoměrně přímočaře a velikost jeho rychlosti se mění pouze při odrazu na pohyblivé stěně, kde se může urychlit nebo zpomalit, podle toho, na kterou stranu se zrovna stěna při dopadu pohybuje.

Na obrázku 5 je znázorněn tzv. fázový portrét tohoto modelu. Ve vodorovném směru je vynášen čas modulo periody oscilace pohyblivé stěny a ve svislém směru velikost rychlosti částice při odrazu na nepohyblivé stěně. V barvě je pak kódována příslušnost bodu k jedné trajektorii. Představte si, jak se bod postupně odráží na nepohyblivé stěně a informace o jeho stavu při odrazu vždy jednou barvou vyneseme jako bod do obrázku.


Z obrázku vidíme, že systém se může chovat dvěma rozdílnými způsoby. Buď je jeho energie omezena (křivky připomínající elipsy a vlnovky), nebo se může chaoticky měnit (oblasti zaplněná mnohobarevnými puntíky). Na obrázcích 6 a 7 jsou pak zobrazeny zajímavé výřezy fázového portrétu.
4. Částečný součet
Předchozí ukázky mohu čtenáři připadat příliš komplikované. Text proto uzavřeme zajímavou ukázkou tematicky patřící do předmětu z prvního ročníku BI-ZMA (Základy maematické analýzy).
Objekt, jehož vlastnosti budeme studovat, budiž následující částečný součet komplexní řady
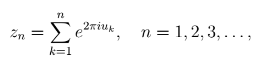
![]()
Tato posloupnost částečných součtů (a tedy i odpovídající řada) není konvergentní. Pozorný čtenář si jistě všiml, že libovolný z jejích sčítanců má absolutní hodnotu rovnu jedné a není proto splněna nutná podmínka konvergence řady.
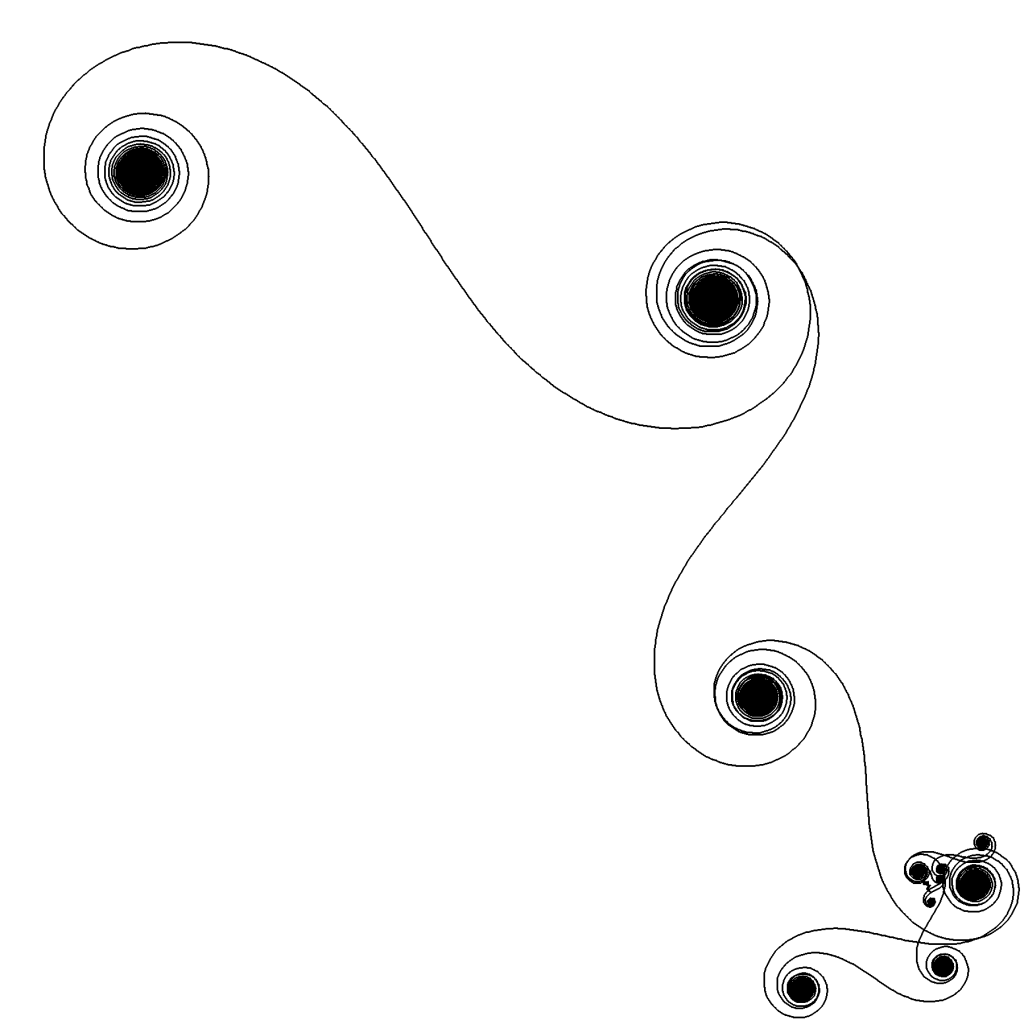
Na obrázku 8 je zobrazeno prvních 50 000 částečných součtů v komplexní rovině. Křivka, kterou vytvářejí, má poměrně zajímavý a neočekávaný tvar.
Autor: Tomáš Kalvoda, KAM FIT ČVUT
