Lasery
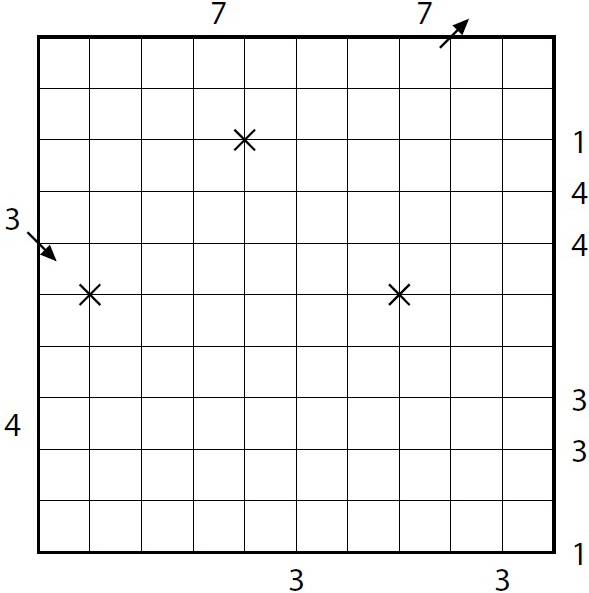
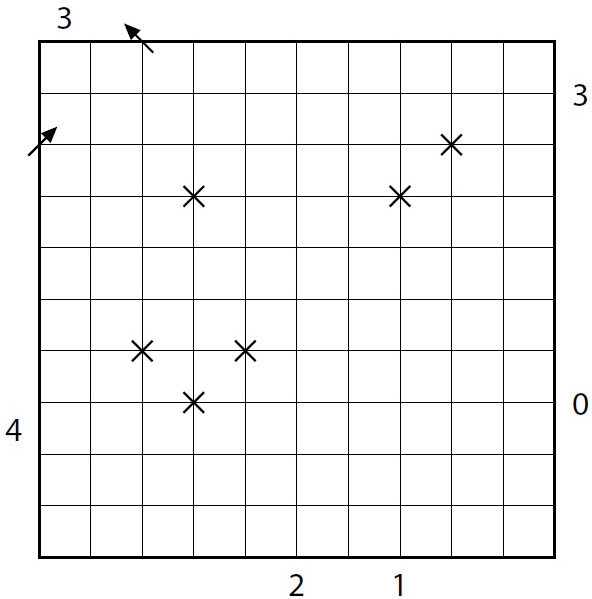
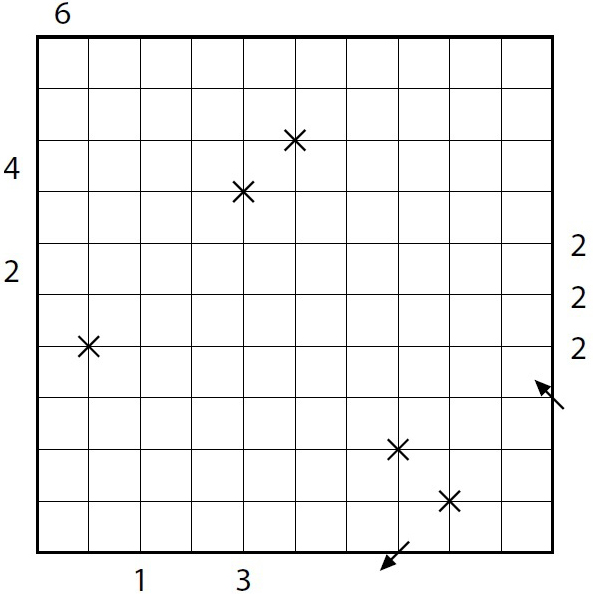
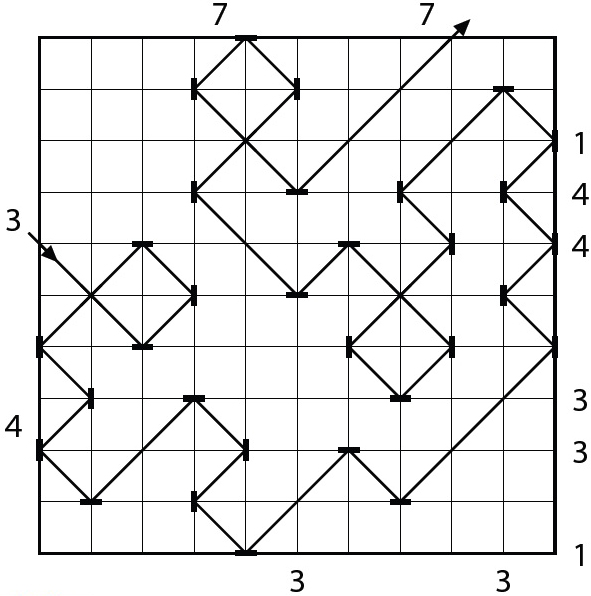
Zakreslete do diagramu jeden laserový paprsek, který probíhá pouze diagonálně a který do diagramu vstupuje a diagram opouští na místě označeném šipkou. Umístěte zrcadla na některé body mřížky tak, aby byl vždy laserový paprsek odražen na jinou stranu.
Čísla na levém okraji a nad diagramem udávají, kolika políčky v odpovídajícím řádku či sloupci paprsky probíhají. Čísla vpravo a pod diagramem určují počet zrcadel na odpovídající linii mřížky. Všechna místa, kde se laser kříží, už jsou označena.
Zadání 1
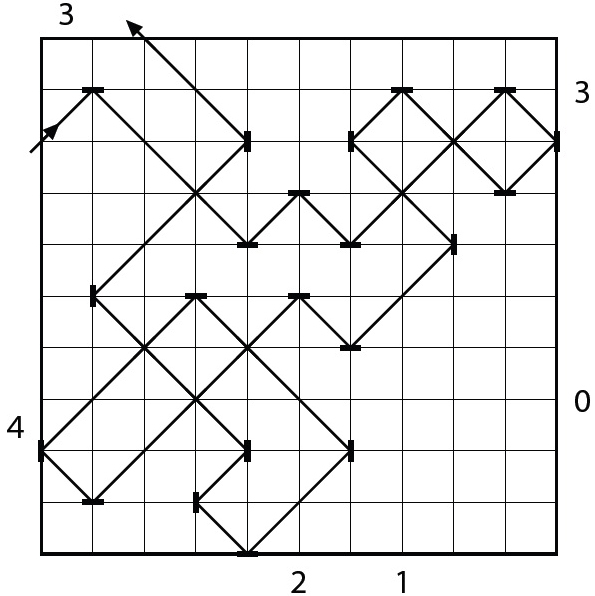
Zadání 2
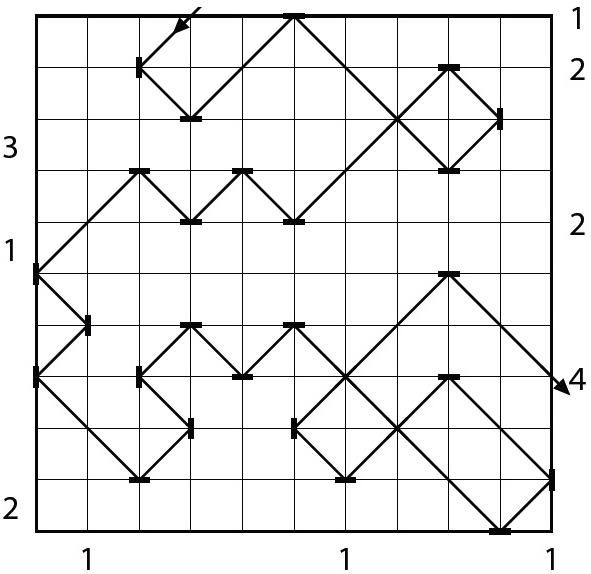
Zadání 3
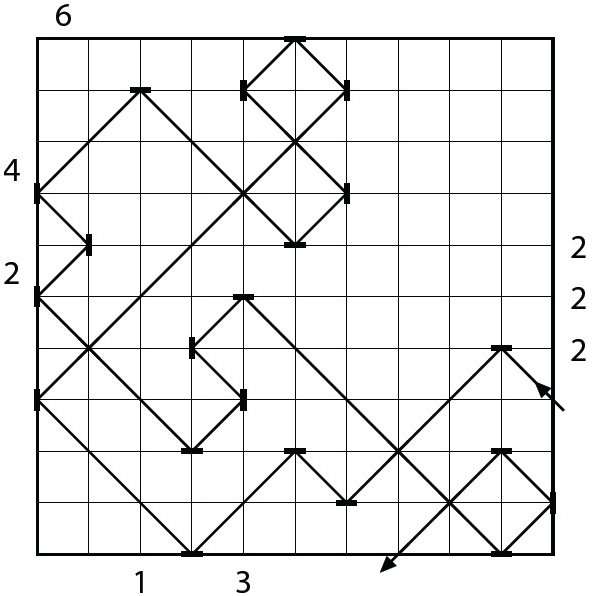
Zadání 4
Řešení 1
Řešení 2
Řešení 3
Řešení 4
Perfektní logici
Hráči A a B dostali oba na své čelo napsáno číslo 12. Jeden vidí číslo na čele druhého a naopak, ale nezná své vlastní. Vedoucí hry jim sdělí, že součet obou jejich čísel je 24 nebo 27 a že se jedná o kladné celé číslo (nula tedy také ne). Poté se vedoucí ptá vždy střídavě hráče A a B, zda mohou určit číslo na svém čele.
A: Ne.
B: Ne.
A: Ne.
B: Ne.
A: Ne.
Po kolika „Ne“ skončí hra, pokud vůbec?
Řešení:
U perfektních logiků uslyšíme sedm „Ne“ a poté „Ano“.
Vysvětlení:
Nechť „a“ je číslo hráče A a „b“ je číslo hráče B.
(1) A ví na začátku, že a = 12 nebo a = 15.
(2) B na začátku ví, že b = 12 nebo b = 15.
Ale B neví, že A ví (1) a A neví, že B ví (2). Proto jsou pro nás vhodnější následující výroky, které jsou oboum hráčům jasné a každý ví, že ten druhý ví:
(3) b = 24 – a nebo b = 27 – a
(4) a = 24 – b nebo a = 27 – b.
Z prvního „Ne“ od hráče A vyplývá právě z (4)
(5) b < 24
neboť v Případě b > 24 by A mohl vyřešit “a”.
To je hnací motor následující cesty řešení:
Z prvního “Ne” od B vyplývá pouze z (3) a (5)
(6) a > 3
a podobně:
A: „Ne“ => b < 21
B: ,,Ne” => a > 6
A: ,,Ne“ => b < 18
B: ,,Ne“ => a > 9
A: ,,Ne” => b < 15
Z toho vyplývá
B: „Ano“
protože dohromady s informací (2) zůstává pouze jedna možnost.
Proto skončí hra po sedmi „Ne“ s následujícím „Ano“.
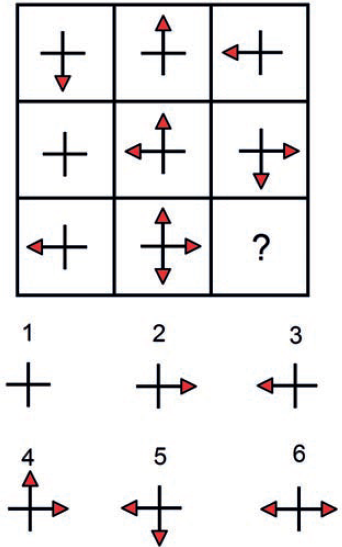
Test
Řešení
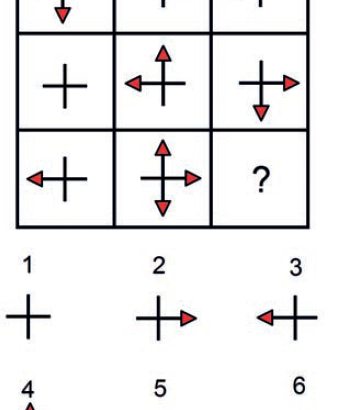
1) 2 – Patří k sobě obrázky 2,6 a 7, dále 3,4 a 8 a poté 1,5 a 9 (popř 2,3,6 a 4,7,8 a 1,5,9). Každá trojice vždy musí pokrýt šipky všech směrů.;
2) 1 – Károvaný vzor se vždy otočí jednou o 180°, jednou o 90°. Kolečka v kruhu také (popř. o 90° a poté o 180°);
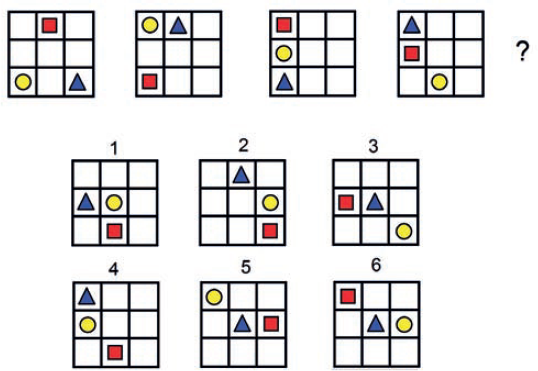
3) 1 – Trojúhelník vždy přijde na místo, kde se nacházel čtverec, čtverec přijde na místo, kde se nacházelo kolečko. Kolečko žádný řád nenásleduje.